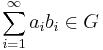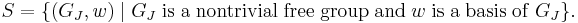Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are also known as formal sums over B. Informally, free abelian groups or formal sums may also be seen as signed multisets with elements in B.
Free abelian groups have very nice properties which make them similar to vector spaces and allow a general abelian group to be understood as a quotient of a free abelian group by "relations". Every free abelian group has a rank defined as the cardinality of a basis. The rank determines the group up to isomorphism, and the elements of such a group can be written as finite formal sums of the basis elements. Every subgroup of a free abelian group is itself free abelian, which is important for the description of a general abelian group as a cokernel of a homomorphism between free abelian groups.
Contents |
Example
For example, let G be the group that is the direct sum  of two copies of the infinite cyclic group
of two copies of the infinite cyclic group 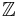 . Symbolically,
. Symbolically,
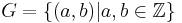 .
.
One basis for this group is {(1,0),(0,1)}. If we say 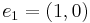 and
and 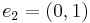 , then we can write the element (4,3) as
, then we can write the element (4,3) as
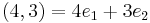 . Where 'multiplication' is defined in following way:
. Where 'multiplication' is defined in following way: 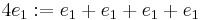 .
.
In this basis, there is no other way to write (4,3), but if we choose our basis to be {(1,0),(1,1)}, where 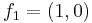 and
and 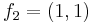 , then we can write (4,3) as
, then we can write (4,3) as
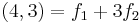 .
.
Unlike vector spaces, not all abelian groups have a basis, hence the special name for those that do. (For instance, any group having periodic elements is not a free abelian group because any element can be expressed in an infinite number of ways simply by putting in an arbitrary number of cycles constructed from a periodic element.) The trivial abelian group {0} is also considered to be free abelian, with basis the empty set.
Terminology
Note that a free abelian group is not a free group except in two cases: a free abelian group having an empty basis (rank 0, giving the trivial group) or having just 1 element in the basis (rank 1, giving the infinite cyclic group). Other abelian groups are not free groups because in free groups ab must be different from ba if a and b are different elements of the basis, while in free abelian groups they must be identical.
Properties
- For every set B, there exists a free abelian group with basis B, and all such free abelian groups having B as basis are isomorphic. One example may be constructed as the abelian group of functions on B, where each function may take integer values, and all but finitely many of its values are zero. This is the direct sum of copies of
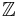 , one copy for each element of B.
, one copy for each element of B. - If F is a free abelian group with basis B, then we have the following universal property: for every arbitrary function f from B to some abelian group A, there exists a unique group homomorphism from F to A which extends f. This universal property can also be used to define free abelian groups.
- Given any abelian group A, there always exists a free abelian group F and a surjective group homomorphism from F to A. This follows from the universal property mentioned above.
- All free abelian groups are torsion-free, and all finitely generated torsion-free abelian groups are free abelian. (The same applies to flatness, since an abelian group is torsion-free if and only if it is flat.) The additive group of rational numbers Q is a (not finitely generated) torsion-free group that's not free abelian. The reason: Q is divisible but non-zero free abelian groups are never divisible.
- Free abelian groups are a special case of free modules, as abelian groups are nothing but modules over the ring
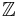 .
.
Importantly, every subgroup of a free abelian group is free abelian (see below). As a consequence, to every abelian group A there exists a short exact sequence
- 0 → G → F → A → 0
with F and G being free abelian (which means that A is isomorphic to the factor group F/G). This is called a free resolution of A. Furthermore, the free abelian groups are precisely the projective objects in the category of abelian groups.[1]
It can be surprisingly difficult to determine whether a concretely given group is free abelian. Consider for instance the Baer–Specker group 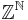 , the direct product (not to be confused with the direct sum, which differs from the direct product on an infinite number of summands) of countably many copies of
, the direct product (not to be confused with the direct sum, which differs from the direct product on an infinite number of summands) of countably many copies of 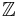 . Reinhold Baer proved in 1937 that this group is not free abelian; Specker proved in 1950 that every countable subgroup of
. Reinhold Baer proved in 1937 that this group is not free abelian; Specker proved in 1950 that every countable subgroup of 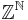 is free abelian.
is free abelian.
Rank
Every finitely generated free abelian group is isomorphic to 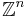 for some natural number n called the rank of the free abelian group. In general, a free abelian group F has many different bases, but all bases have the same cardinality, and this cardinality is called the rank of F. This rank of free abelian groups can be used to define the rank of all other abelian groups: see rank of an abelian group. The relationships between different bases can be interesting; for example, the different possibilities for choosing a basis for the free abelian group of rank two is reviewed in the article on the fundamental pair of periods.
for some natural number n called the rank of the free abelian group. In general, a free abelian group F has many different bases, but all bases have the same cardinality, and this cardinality is called the rank of F. This rank of free abelian groups can be used to define the rank of all other abelian groups: see rank of an abelian group. The relationships between different bases can be interesting; for example, the different possibilities for choosing a basis for the free abelian group of rank two is reviewed in the article on the fundamental pair of periods.
Formal sum
A formal sum of elements of a given set B is an element of the free abelian group with basis B. In other words, given a set B, let G be the unique (up to isomorphism) free abelian group with basis B. For elements 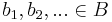 and
and 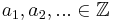 (where there may be an
(where there may be an 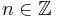 such that
such that 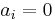 iff
iff 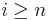 ),
),
Subgroup closure
Every subgroup of a free abelian group is itself a free abelian group. This is similar to the Nielsen–Schreier theorem that a subgroup of a free group is free.[2]
Theorem: Let  be a free abelian group generated by the set
be a free abelian group generated by the set 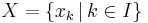 and let
and let 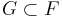 be a subgroup. Then
be a subgroup. Then  is a free abelian group.
is a free abelian group.
Proof:[3] If 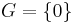 , the statement holds, so we can assume that
, the statement holds, so we can assume that  is nontrivial. First we shall prove this for finite
is nontrivial. First we shall prove this for finite  by induction. When
by induction. When 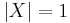 ,
,  is isomorphic to
is isomorphic to 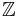 (being nontrivial) and clearly free. Assume that if a group is generated by a set of size
(being nontrivial) and clearly free. Assume that if a group is generated by a set of size 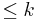 , then every subgroup of it is free. Let
, then every subgroup of it is free. Let 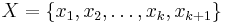 ,
,  the free group generated by
the free group generated by  and
and 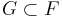 a subgroup. Let
a subgroup. Let 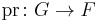 be the projection
be the projection 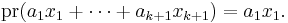 If
If 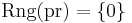 , then
, then  is a subset of
is a subset of 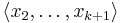 and free by the induction hypothesis. Thus we can assume that the range is nontrivial. Let
and free by the induction hypothesis. Thus we can assume that the range is nontrivial. Let 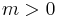 be the least such that
be the least such that 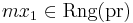 and choose some
and choose some  such that
such that 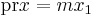 . It is standard to verify that
. It is standard to verify that 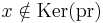 and if
and if 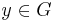 , then
, then 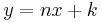 , where
, where 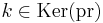 and
and 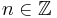 . Hence
. Hence 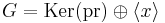 . By the induction hypothesis
. By the induction hypothesis 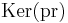 and
and 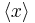 are free: first is isomorphic to a subgroup of
are free: first is isomorphic to a subgroup of 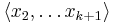 and the second to
and the second to 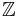 .
.
Assume now that 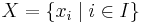 is arbitrary. For each subset
is arbitrary. For each subset  of
of  let
let 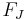 be the free group generated by
be the free group generated by 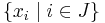 , thus
, thus 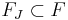 is a free subgroup and denote
is a free subgroup and denote 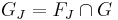 .
.
Now set
Formally  is an injective (one-to-one) map
is an injective (one-to-one) map
such that ![w[J']](/2012-wikipedia_en_all_nopic_01_2012/I/65e05c048cec5bc7f64c6d87d95860b7.png) generates
generates 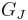 .
.
Clearly  is nonempty: Let us have an element
is nonempty: Let us have an element  in
in  . Then
. Then 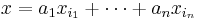 and thus the free group generated by
and thus the free group generated by 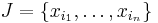 contains
contains  and the intersection
and the intersection  is a nontrivial subgroup of a finitely generated free abelian group and thus free by the induction above.
is a nontrivial subgroup of a finitely generated free abelian group and thus free by the induction above.
If 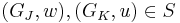 , define order
, define order 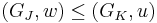 if and only if
if and only if 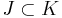 and the basis
and the basis  is an extension of
is an extension of  ; formally if
; formally if 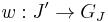 and
and 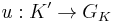 , then
, then 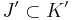 and
and 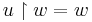 .
.
If 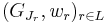 is a
is a 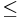 -chain (
-chain ( is some linear order) of elements of
is some linear order) of elements of  , then obviously
, then obviously
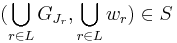 ,
,
so we can apply Zorn's lemma and conclude that there exists a maximal 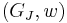 . Since
. Since 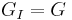 , it is enough to prove now that
, it is enough to prove now that 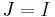 . Assume on contrary that there is
. Assume on contrary that there is 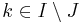 .
.
Put 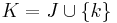 . If
. If 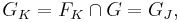 then it means that
then it means that 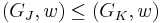 , but they are not equal, so
, but they are not equal, so 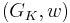 is bigger, which contradicts maximality of
is bigger, which contradicts maximality of 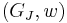 . Otherwise there is an element
. Otherwise there is an element 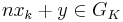 such that
such that 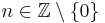 and
and 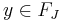 .
.
The set of 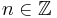 for which there exists
for which there exists 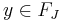 such that
such that 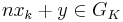 forms a subgroup of
forms a subgroup of 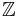 . Let
. Let 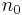 be a generator of this group and let
be a generator of this group and let 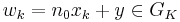 with
with 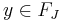 . Now if
. Now if 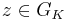 , then for some
, then for some 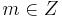 ,
, 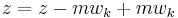 , where
, where 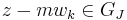 .
.
On the other hand clearly 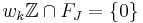 , so
, so 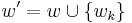 is a basis of
is a basis of 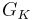 , so
, so 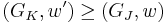 contradicting the maximality again.
contradicting the maximality again. 
See also
Notes
- ^ Griffith, p.18
- ^ According to Johnson, this result is due to Richard Dedekind. Johnson, D. L. (1980). Topics in the Theory of Group Presentations. London Mathematical Society lecture note series. 42. Cambridge University Press. p. 9. ISBN 9780521231084.
- ^ This proof is an application of Zorn's lemma and can be found in Appendix 2 §2, page 880 of Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR1878556.
References
- Phillip A. Griffith (1970). Infinite Abelian group theory. Chicago Lectures in Mathematics. University of Chicago Press. ISBN 0-226-30870-7.